Talk on Locally Stationary Processes -- From Approximations to Statistical Inference

Abstract

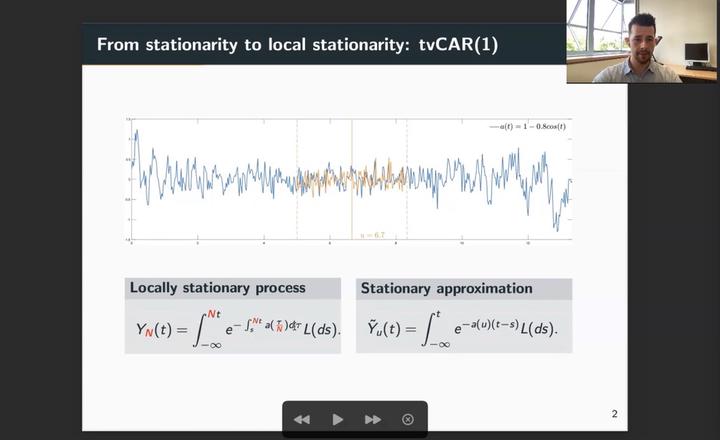
We introduce a general theory on stationary approximations for locally stationary continuous-time processes. Based on the stationary approximation, we use θ-weak dependence to establish laws of large numbers and central limit type results under different observation schemes. Hereditary properties for a large class of finite and infinite memory transformations show the flexibility of the developed theory and are used to establish asymptotic properties of M-estimators. As examples we consider time-varying Ornstein-Uhlenbeck processes and time-varying Lévy-driven state space models, for which we introduce a localized quasi maximum likelihood estimator. A simulation study shows the applicability of the estimation procedure.

Bennet Ströh

Postdoctoral researcher

I am a postdoctoral researcher at the Department of Mathematics at Imperial College London and research associate at the Alan Turing Institute.